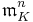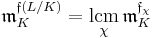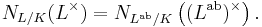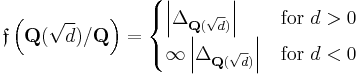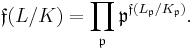Conductor (class field theory)

In algebraic number theory, the conductor of a finite abelian extension of local or global fields provides a quantitative measure of the ramification in the extension. The definition of the conductor is related to the Artin map.

1 Local conductor
- 1.1 More general fields
- 1.2 Archimedean fields
2 Global conductor
- 2.1 Algebraic number fields
  - 2.1.1 Example
  - 2.1.2 Relation to local conductors and ramification
3 Notes
4 Reference

Local conductor

Let L/K be a finite abelian extension of non-archimedean local fields. The conductor of L/K, denoted 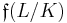$\mathfrak{f}(L/K)$ , is the smallest non-negative integer n such that the higher unit group 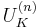$U_K^{(n)}$ is contained in N_L_/K(L^×), where N_L_/K is field norm map.^[1] Equivalently, n is smallest such that the local Artin map is trivial on 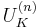$U_K^{(n)}$ . Sometimes, the conductor is defined as

$\mathfrak{m}_K^n$

where n is as above and 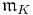$\mathfrak{m}_K$ is the maximal ideal of K.^[2]

The conductor of an extension measures the ramification. Qualitatively, the extension is unramified if, and only if, the conductor is zero,^[3] and it is tamely ramified if, and only if, the conductor is 1.^[4] More precisely, the conductor computes the non-triviality of higher ramification groups: if s is the largest integer for which the "lower-numbering" higher ramification group G_s is non-trivial, then 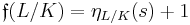$\mathfrak{f}(L/K)=\eta_{L/K}(s)%2B1$ , where η_L/K is the function that translates from "lower-numbering" to "upper-numbering" of higher ramification groups.^[5]

The conductor of L/K is also related to the Artin conductors of characters of the Galois group Gal(L/K). Specifically,^[6]

$\mathfrak{m}_K^{\mathfrak{f}(L/K)}=\underset{\chi}{\mathrm{lcm}}\,\mathfrak{m}_K^{\mathfrak{f}_\chi}$

where χ varies over all multiplicative complex characters of Gal(L/K), 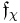$\mathfrak{f}_\chi$ is the Artin conductor of χ, and lcm is the least common multiple.

More general fields

The conductor can be defined in the same way for L/K a not necessarily abelian finite Galois extension of local fields.^[7] However, it only depends on L^ab/K, the maximal abelian extension of K in L, because of the "norm limitation theorem", which states that, in this situation,^[8]^[9]

$N_{L/K}(L^\times)=N_{L^{\text{ab}}/K}\left((L^{\text{ab}})^\times\right).$

Additionally, the conductor can be defined when L and K are allowed to be slightly more general than local, namely if they are complete valued fields with quasi-finite residue field.^[10]

Archimedean fields

Mostly for the sake of global conductors, the conductor of the trivial extension R/R is defined to be 0, and the conductor of the extension C/R is defined to be 1.^[11]

Global conductor

Algebraic number fields

The conductor of an abelian extension L/K of number fields can be defined, similarly to the local case, using the Artin map. Specifically, let θ : I^m → Gal(L/K) be the global Artin map where m is a defining modulus for L/K, then the conductor of L/K, denoted 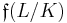$\mathfrak{f}(L/K)$ , is the smallest modulus such that θ factors through the ray class group modulo 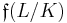$\mathfrak{f}(L/K)$ .^[12]^[13] It can also be defined as the greatest common divisor of all defining moduli of θ.

Example

Let p be a prime number and let L/K be 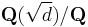$\mathbf{Q}(\sqrt{d})/\mathbf{Q}$ where d is a squarefree integer. Then,^[14]

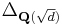$\mathfrak{f}\left(\mathbf{Q}(\sqrt{d})/\mathbf{Q}\right) = \begin{cases} \left|\Delta_{\mathbf{Q}(\sqrt{d})}\right| & \text{for }d>0 \\ \infty\left|\Delta_{\mathbf{Q}(\sqrt{d})}\right| & \text{for }d<0 \end{cases}$

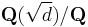where $\Delta_{\mathbf{Q}(\sqrt{d})}$ is the discriminant of $\mathbf{Q}(\sqrt{d})/\mathbf{Q}$ .

Relation to local conductors and ramification

The global conductor is the product of local conductors:^[15]

$\displaystyle \mathfrak{f}(L/K)=\prod_\mathfrak{p}\mathfrak{p}^{\mathfrak{f}(L_\mathfrak{p}/K_\mathfrak{p})}.$

As a consequence, a finite prime is ramified in L/K if, and only if, it divides 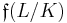$\mathfrak{f}(L/K)$ .^[16] An infinite prime v occurs in the conductor if, and only if, v is real and becomes complex in L.

Notes

^ Serre 1967, §4.2
^ As in Neukirch 1999, definition V.1.6
^ Neukirch 1999, proposition V.1.7
^ Milne 2008, I.1.9
^ Serre 1967, §4.2, proposition 1
^ Artin & Tate 2009, corollary to theorem XI.14, p. 100
^ As in Serre 1967, §4.2
^ Serre 1967, §2.5, proposition 4
^ Milne 2008, theorem III.3.5
^ As in Artin & Tate 2009, §XI.4. This is the situation in which the formalism of local class field theory works.
^ Cohen 2000, definition 3.4.1
^ Milne 2008, remark V.3.8
^ Some authors omit infinite places from the conductor, e.g. Neukirch 1999, §VI.6
^ Milne 2008, example V.3.11
^ For the finite part Neukirch 1999, proposition VI.6.5, and for the infinite part Cohen 2000, definition 3.4.1
^ Neukirch 1999, corollary VI.6.6

Reference

Artin, Emil; Tate, John (2009) [1967], Class field theory, American Mathematical Society, ISBN 978-0-821-84426-7, MR 2467155
Cohen, Henri (2000), Advanced topics in computational number theory, Graduate Texts in Mathematics, 193, Springer-Verlag, ISBN 978-0-387-98727-9
Milne, James (2008), Class field theory (v4.0 ed.), http://jmilne.org/math/CourseNotes/cft.html, retrieved 2010-02-22
Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR 1697859
Serre, Jean-Pierre (1967), "Local class field theory", in Cassels, J. W. S.; Fröhlich, Albrecht, Algebraic Number Theory, Proceedings of an instructional conference at the University of Sussex, Brighton, 1965, London: Academic Press, ISBN 0-121-63251-2, MR 0220701